尚絅学院高校：数学の「合格勉強法 & お薦めの参考書」
皆さん、こんにちは。 仙台市で東北大生家庭教師を派遣している「名門進学会」、社長の三沢 也寿志（みさわ やすし・早大大学院修了）です。
1. 前書き
今日は、尚絅学院高校を目指す受験生とその親御さんのために、数学の「合格勉強法＆お薦めの参考書」をご紹介します。 お役に立ちますので、該当する方は最後までお読み下さい。
2. 過去問の入手と演習
過去問は同校のホームページに掲載されているので、受験年度の早い時期に入手（プリントアウト）して下さい。 そして、すぐに一度解いて下さい。 中学3年生の早い時期であれば余り解けないかも知れませんが、別に目的があるのでそれはほとんど気にする必要がありません。
2024年・A日程入試問題の一部
的を絞った勉強が出来る
その目的とは、生徒さんに早い時期に一度過去問（本試験と出題傾向が一番似ています）を解いてもらうことによって、同校入試ではどのような傾向の問題が出題されているのかを把握してもらうことです。 なぜならば、出題傾向を把握出来れば、その後はそれに合わせて的を絞った勉強をすることが出来るからです。
3. 計算問題対策
文理・税込1,430円
この参考書には中1・中2の分もあります（それぞれ同価格）。
難しくないので
同校入試の数学では、大問1として計算問題が7個あります。 これらは、思考能力をあまり必要としない分他の問題と比べて難しくないので、確実に得点したいところです。
対策としては、章の初めに解き方が載っている分かりやすい参考書兼問題集で十分に演習を行うことです。 上の本は総合的・まとめ的なものですが、ここではお薦めです。
4. 図形問題対策
受験研究社・税込3,245円
まず図形の性質を覚えて
図形問題は、A日程・B日程とも大問が一つ（大問6）と大問2の中で小問が一つ（その中に枝問が二つ）出題されています。 対策としては、教科書や適切な参考書でそれぞれの図形の性質を覚えて、それから多くの問題を解いてみることです。
図形に特化した良い参考書が見当たらなかったので、総合的な参考書の中で図形の分野が充実している上の本をお薦めします。 また問題集としては、上記 3. でお勧めした本の図形分野の問題などもお薦めです。
5. 図形と関数・グラフの融合問題対策
東京学参・税込1,650円
適切な参考書で解き方を学び
図形と関数・グラフの融合問題は、A日程・B日程とも大問5で出題されています。 対策としては、適切な参考書で解き方を学び、それから演習を重ねて下さい。 参考書兼問題集としては、初版年度が古いですが上の本をお薦めします。
6. 確率・統計問題対策
文英堂・税込803円
時間を掛けないで解くためには
A日程・B日程とも確率の問題は大問4すべてで、統計の問題は大問3の中の小問1つ（枝問は4個）で出題されています。 統計の問題は基本的な知識があれば解けるものばかりですが、時間を余り掛けないで同校の確率の問題を解くためには、十分な知識と思考能力が必要です。
よく読んで繰り返し演習して
そのための参考書としては、上の本をお薦めします。 文庫本サイズの小さなものですが、高校入試の確率・統計で必要な知識と計算方法がカラフルで分かりやすく網羅されています。 この本をよく読んで知識を身に付け、そして繰り返し演習して下さい。
7. 最後は過去問を解きまくる
最後に、入試まであと3か月になったら、その後は過去問を解きまくって下さい。 同校のホームページからダウンロード可能なすべての過去問を何度も解いて、ほとんどの問題を出来るようにしてから受験に臨んで下さい。 そうすれば、本番でも間違いなく高得点を取れます。
東北学院高校：数学の「合格勉強法 & お薦めの参考書」
皆さん、こんにちは。 仙台市で東北大生家庭教師を派遣している「名門進学会」、社長の三沢 也寿志（みさわ やすし・早大大学院修了）です。
1. 前書き
今日は、東北学院高校を目指す受験生とその親御さんのために、数学の「合格勉強法＆お薦めの参考書」をご紹介します。 お役に立ちますので、該当する方は最後までお読み下さい。
2. 過去問の入手と演習
過去問は同校のホームページに掲載されているので、受験年度の早い時期に入手（プリントアウト）して下さい。 そして、すぐに一度解いて下さい。 中学3年生の早い時期であれば余り解けないかも知れませんが、別に目的があるのでそれはほとんど気にする必要がありません。
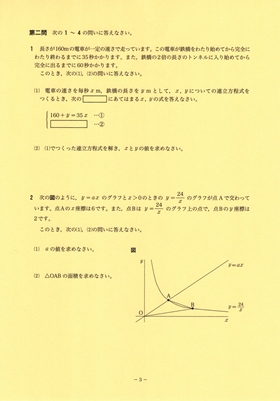
2025年・A日程入試問題の一部
的を絞った勉強が出来る
その目的とは、生徒さんに早い時期に一度過去問（本試験と出題傾向が一番似ています）を解いてもらうことによって、同校入試ではどのような傾向の問題が出題されているのかを把握してもらうことです。 なぜならば、出題傾向を把握出来れば、その後はそれに合わせて的を絞った勉強をすることが出来るからです。
3. 計算問題対策
文理・税込1,430円
この参考書には中1・中2の分もあります。
取り組みやすいので
同校入試の数学では、大問1として計算問題が6～9個くらいあります。 これらの計算問題は、思考能力をあまり必要としない分他の問題と比べて取り組みやすいので、確実に得点したいところです。
対策としては、章の初めに解き方が載っている分かりやすい参考書兼問題集で十分に演習を行うことです。 上の画像の本は総合的・まとめ的なものですが、ここではお薦めです。
4. 図形問題対策
受験研究社・税込3,245円
まず図形の性質を覚えて
図形問題は、3種類の入試とも大問が一つ（大問4）と小問がいくつか出題されています。 対策としては、教科書や適切な参考書でそれぞれの図形の性質を覚えて、それから多くの問題を解いてみることです。
図形に特化した良い参考書が見当たらなかったので、総合的参考書の中で図形の分野が充実している上の本をお薦めします。 また問題集としては、上記 3. でお勧めした本の図形分野の問題などもお薦めです。
5. 図形と関数・グラフの融合問題対策
東京学参・税込1,650円
適切な参考書で解き方を学び
図形と関数・グラフの融合問題は、大問2の中の小問（枝問が2つ）で出題されます。 また、この他に大問3で出題されることもあります。 その対策としては、適切な参考書で解き方を学び、それから演習を重ねることです。 参考書兼問題集として、初版年度が古いものではありますが上の本をお薦めします。
6. 図形の証明問題対策
くもん出版・税込1540円
小問が一つだけなので
図形の証明問題は、大問4（すべてが図形の問題）の中で小問として1つだけ出題されています。 同校入試ではそれだけなので時間を掛ける必要はありませんが、他校の入試でも（もちろん公立高校の入試でも）出題される問題なので、時間がある方は上の本で対策をしておいて下さい。
7. 最後は過去問を解きまくる
最後に、入試まであと3か月になったら、その後は過去問を解きまくって下さい。 同校のホームページからダウンロード可能なすべての過去問を何度も解いて、ほとんどの問題を出来るようにしてから受験に臨んで下さい。 そうすれば、本番でも間違いなく高得点を取れます。
仙台市立中学校の数学：社長お薦めの参考書×4
皆さん、こんにちは。 仙台市で東北大生家庭教師を派遣している「名門進学会」、社長の 三沢 也寿志（みさわ やすし・早大大学院修了）です。
1. 前書き
今日は、仙台市立中学校の生徒さんとその親御さんのために、数学の成績がアップする参考書4冊を以下の 2.～5. でご紹介します（2025年7月改訂済）。 当社でたくさん購入した参考書類から選び抜いたものなので、必ずやお役に立つでしょう。 該当する方はぜひ最後までご覧下さい。
2. 教科書ガイド・東京書籍版
あすとろ出版・税込2,970円：もちろん中1・中2用も出版されています。
教科書の内容を分かりやすく
教科書ガイドとは、教科書の内容をかみ砕いて分かりやすく解説してくれる書籍で、教科書に記載の問題の解答や解法も詳しく記載されています。 ですから、この本を読めば、授業だけではよく分からなかった個所や問題・授業では触れられなかった箇所や問題を理解する助けとなります。
中学生向けの学習参考書としては決して安いものではありませんが、Amazonなどで普通に買える本なので、生徒さんが家庭学習を効率的に行うためにお手許に置いておくことを強くお勧めします。
3. まとめ的参考書
文理・税込1,430円：もちろん中1・中2用も出版されています。
カラフルで楽しく
中学校各学年の数学で覚えなければならない事柄が、項目別に分かりやすくまとめられている参考書です。 中身がとてもカラフルなので、勉強があまり好きではない中学生でもこの本を使って勉強するのが楽しくなってしまうかもしれません。
上記のように1冊（1学年分）1,430円と値段も安く、Amazonなどで普通に買えるし、かつ項目ごとに知識定着のためのステップを踏んだ問題も併せて記載されているので、この書籍も僕のお薦めです。
4. 文章題の参考書
くもん出版・税込1,540円
問題を解きながら学ぶ
中学校数学の中の「文章題」に特化した参考書です。 まず、各項目の初めに「要点チェック」として公式やちょっとした解法などが書いてあります。 そして次に『問題（例題）を、手順を踏みながら解いて、その過程で当該文章題の解法を学ぶ』という形式になっています。
問題演習というアウトプットを行いながら学ぶという方法は、読むだけ（インプットだけ）の学習よりも記憶の歩留まりが良くなります。 そして、数学の文章題を苦手とする中学生が多いことから、この参考書（＆問題集）もお薦めです。
5. 図形の証明問題の参考書
くもん出版・税込1,540円
上記 4. の参考書と同じ出版社のもので、中学校数学の中の「図形の証明問題」に特化した参考書です。 こちらも「要点チェック」に図形の定義や公式が記載されています。 そして次に『問題（例題）を、手順を踏みながら解いて、その過程で当該図形の証明問題の解法を学ぶ』という形式になっています。
4. の場合と同様に、読者がこの本でも行うことになるアウトプットを伴う学習は記憶の歩留まりが良く、また「図形の証明問題」も「文章題」同様苦手とする中学生が多いことから、この参考書（＆問題集）も僕のお薦めです。
科目別「予習」&「復習」の最適な時間配分
受験生の皆さん、お久しぶりです！ 仙台市の『名門進学会』家庭教師で「東北大学医学部医学科」3年の 金子 茉央（かねこ まお）です。
1.「予習」or「復習」
自分自身の勉強の経験と色んな人に勉強を教えた経験から、最近ふと気づいたことがあります。 それは、自分自身の勉強時間をどのくらい「予習」と「復習」に割くかが人によって違う、ということです。 勉強スタイルは人それぞれですが、私が大事だと思った「勉強時間の配分」についてお話しします。
2. 3段階の勉強サイクル
理想の勉強サイクルとは、「予習をする」「授業時間内で理解して間違いを正す」「復習をする」という3段階で学習をすることです。 まあ、行うのが難しいから理想というのですが… 要領が良くて全科目で十分にこれらを行う余裕のある人は、ぜひやってみて欲しいです。
教科書を読んでの予習
多分、飛躍的に成績は伸びるし、勉強に困ることは少なくなると思います。 しかし、大抵の人はそんな時間はないと思います。 少なくとも、私が「多分」と書いたのは、自分ではその余裕がなかったからです。 時間のない皆さんは、科目ごとにメリハリをつけることをお勧めします。
3. 科目別優先順位
A. 国語
正直言って、あまり勉強時間を割いた覚えがないです。 ですが、3段階の中で一番大事にしていたのは、「授業内での先生の解説」です。 国語は、文章内の手がかりからどう文章を解釈し、考察していくかの科目ですので、先生の解釈の根拠を知ることが大事です。 授業中のメモが、テスト前に生きてきます。
B. 数学
理系ですので、一番時間を割いていました。 数学は、3段階の中で圧倒的に復習が大事です。 私は、一番効率的な解き方や公式の導出を知らずにゴリゴリ解くのが嫌いだったので、新しい問題を習う時に予習はあえてほとんどしませんでした。
問題集を解いたノート
授業時間は、公式のインプットです。 ですが、数学はアウトプットが出来なくては立ち行きません。 そして、アウトプットに必要なのは演習です。 私の高校では、問題集があらかじめ配布されていたので、授業で習った範囲の問題集をすぐに解くようにしていました。
C. 理科
理科も同様に、復習に時間を最も割いていました。 でも、結構授業時間内の学習が大事です。 先生がその科目へ情熱を語る人だったら、言ったことは全部メモしましょう。
理科は日常生活と深く結びついているので、問題を解きながら「あのことだな！」と思えると記憶の定着率が全く異なります。 面白いと思った人の勝ちです。 物理や化学は問題を解けるようにしなくてはならないので、しっかりアウトプット出来るように沢山復習して下さい。
理科の参考書の例
D. 社会
私は、授業時間の学習を一番大事にしていました。 また、暗記科目なので、家に帰った後一度は目を通すとテスト前少し楽になります。 ただ、現役時はそこまで多くの時間は割くことは出来ませんでした。
E. 英語
予習が一番大事です。 個人的な意見ですが、答え（和訳等）を知ってしまった後の復習はそんなに意味がないと思っています。
英語の教科書の例
予習段階で自分の力で構文を読み解き意味を考え、授業時間内で答え合わせをして、自分でやった和訳との食い違いを知るのが勉強の流れです。 逆に、予習をしなければクイズの答えを延々と聞いているだけの状態になり、授業の価値が半減してしまうと思います。
以上、私の経験からではありますが、参考になれば幸いです。
東大などの数学：考え方と解法
受験生の皆さん、こんにちは！ 仙台市の『名門進学会』家庭教師で東北大学医学部医学科2年の 金子 茉央（かねこ まお）です
1. お疲れ様でした！
皆さんは、怒涛の日々が過ぎ去り、ようやく一息つけた頃でしょうか？ 中には、気持ちを切り替えて、後期試験に向けて勉強に取り組んでいる方もいらっしゃるのでしょうか？ 何はともあれ、本当にお疲れ様でした。（2026年4月に以下を加筆・修正）
サクラ咲ケの赤べこ
2. 難問に挑戦した過去
皆さんは、東大の問題を解いたことありますか？ 一度触れたことがある人ならお分かりだと思いますが、東大の問題は期待を裏切らずものすごく難しいです。 私の志望校は高3の春に決まりましたが、難問を解く力を身につけるべく東大・京大・東京科学大といった難問を出すことで有名な大学の問題も積極的に解いていました。
東京大学・赤門
受験目前には東大の問題でも
中には何度問題文を読んでも手も足も出ない問題すらあって、始めの頃は気が遠くなるような思いをしたことをよく覚えています。 でも、私は受験を目前に控えた頃には、東大の問題に対して以前のような忌避感を感じなくなっていました。
3. 難問を解くときの考え方・解法
どうしてなのか？ そこで、今回は、「数学」や「理科」の難しい問題を解く時の考え方や解法についてお話ししていきます。
A.「難問」へのアプローチ
「難問」と言われる問題は、何がその問題を難問たらしめているのでしょうか？ いかに大学の教授が作った難しい問題といえども、高校生の知っている知識や公式で解けなくてはなりません。 高校生の知っている知識や公式を用いて解くことの出来る数学の典型は、すなわちチャートの例題です。
青チャートの例
使ったことのある人ならお分かりだと思いますが、チャート（私は青チャートを使っていました）は、公式ごとに定型の問題文に対して、最も効率の良い解き方が示されています。 そして私は、ほとんどの難問は何らかの閃きや解釈によって、これらのパターン問題に「落とし込む」ことが出来ると思っています。
B. 知っている問題に「落とし込む」
手も足も出ないのは、自分が見たことがない問題だからです。 ならば、自分の知っている「チャートのパターン問題に落とし込める」ように頑張れば良いのです。 そう考え始めてからは、見たことのない問題であっても「解ける訳がない！」という忌避感を感じなくなりました。
いわゆる難関校の問題は
とは言っても、青チャートの例題はしっかりやり込めば偏差値60くらいになるので、パターン問題と言っても皆が解けるわけではありません。 そこを当たり前に解けるものとして提示してくるのが、いわゆる難関校の問題であるように感じます。
難関校の問題・赤本
C. 自分にあったレベルから着実に
今、難関校の問題が全く解けないと感じる人は、是非とも「自分がどの段階でつまずいているのか」解答を読んで確かめて下さい。 難問を自分の知っているパターン問題に落とし込む所で手こずっているのか、それとも次の段階のパターン問題をきちんと身につけていないのか。
よく使っていた問題集
もう一度解き直して
後者である場合は、チャートレベルの問題集を今一度解き直して下さい。 数学の問題集は、無闇に難易度の高いものに手を出してはいけません。 難しい問題集は、その1ランク下の問題集が解けることを前提として構成されていますから、それがきちんと解けるようになってから次に進むべきです。
忌避感を和らげられたら
難問への取り組み方について自分なりの考え方をお伝えしてきましたが、いかがでしたでしょうか？ もちろんこれは1個人の意見なので、皆さんも自分なりの考え方で難問にアプローチして頂ければと思います。 私の勉強法で、皆さんの忌避感を少しでも和らげられたら幸いです。
