
図形問題とその攻略法
二華中学校入試問題の中では、最も難易度が高いと感じました。 それでも、ある程度点数を取れるようになっていかないと周りに差をつけることができません。 令和4年度の問題では以下の問題が該当します。
| 大問1-2 | (2) | 車の工作 |
| 大問2-3 | (2) | 花壇の分割 |
| (3) | 面積計算 |
解説
大問1-2(2)
展開図から、窓Aと窓Bがどのような位置に来るのかを把握する必要があります。 図形問題の鉄則は、書き込むことです。 以下に、私の書き込みの例を示します。
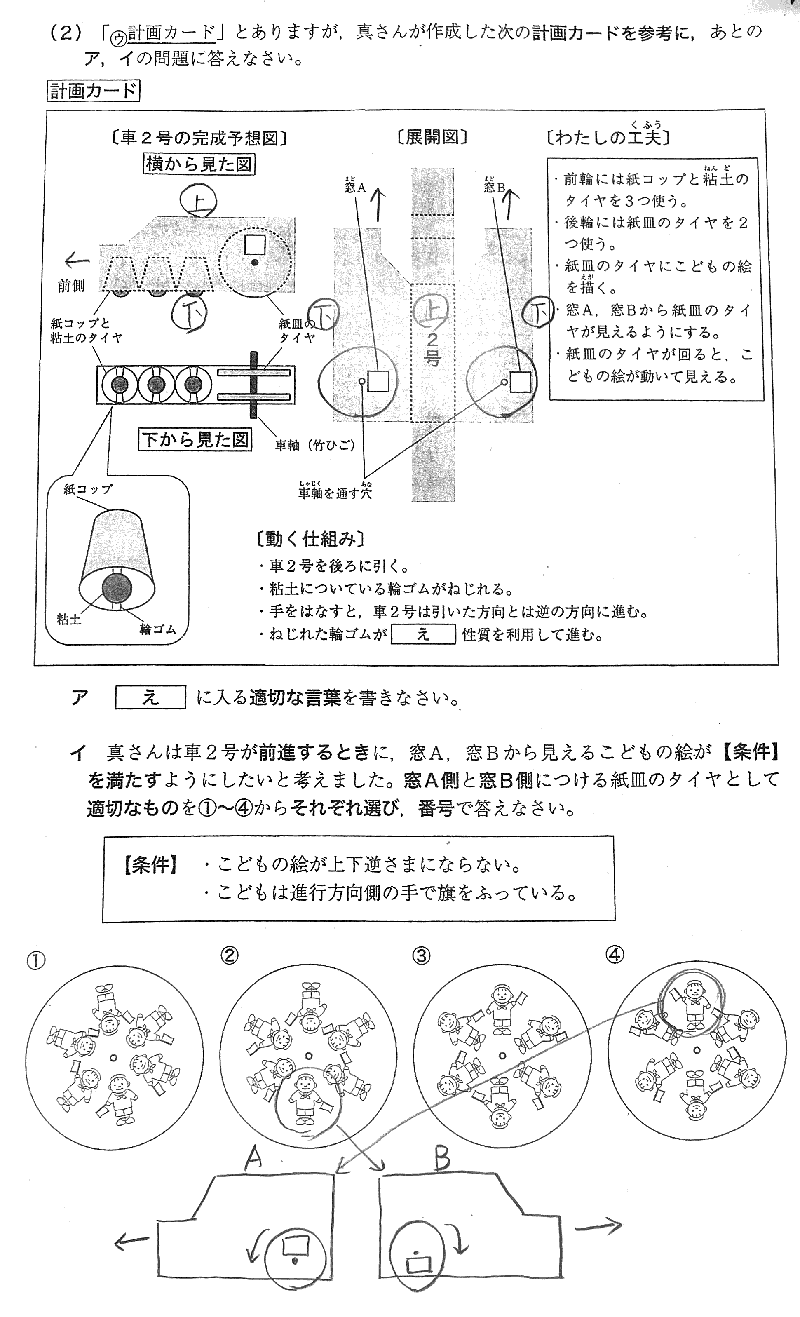
いかがでしょうか? 上記のように書き込めば、自信を持って窓Aに対応するのは④、窓Bに入るのは②だということができます。
大問2−3(2)
唯一の証明問題です。 証明問題は部分点がもらえるので、分かる範囲だけでも書くようにしましょう。
図形問題の鉄則の1つ目は書き込むことだとお話ししましたが、2つ目は適切な補助線を引くことです。 問題を通して具体的に説明していきます。
今回の問題では、長方形A B C Dの中にポツンと点Eがふられています。 こういう中途半端な点を見つけたら、とりあえず周りと平行な線を引きましょう。 色々なことが見えてくるはずです。
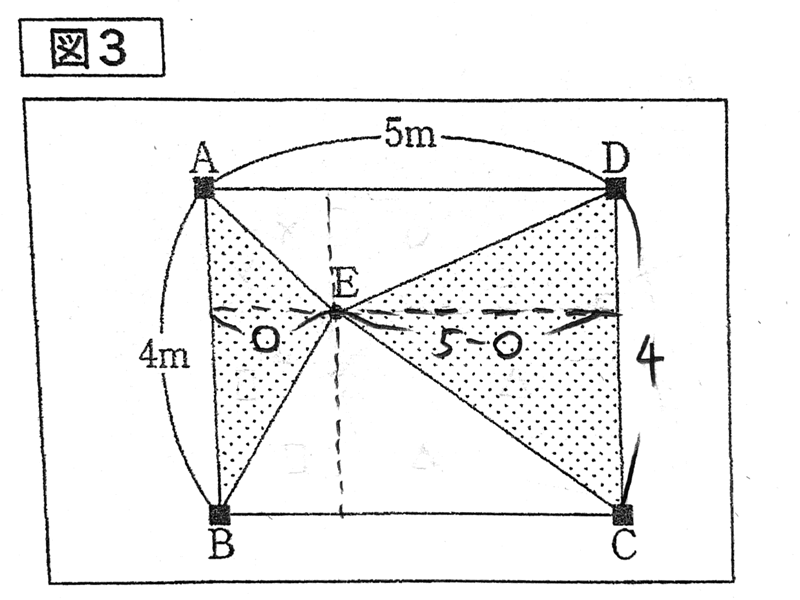
三角形A B Eにおいて、底辺をA Bとして高さを○とおく。 また、三角形C D Eにおいて底辺をC Dとして高さを5―○とおくと、面積はそれぞれ以下のようになります。
- 三角形A B Eの面積は4×○÷2
- 三角形C D Eの面積は4×(5―○)÷2
2つの三角形の面積を足すと、4×(○+5―○)÷2=10m2
長方形A B C Dの面積は4×5=20m2ですので、半分の面積であることが証明されます。
大問2−3(3)
難問です。 でも諦めないで下さい。 なぜなら、この問題は(3)だからです。 連問は、往々にして一つ前の問題がヒントになっていることが多いです。 問題を通して具体的に説明していきます。
まずは図形問題の鉄則を思い出しましょう。1つ目は情報を全て書き込むことで、2つ目は適切な補助線を引くことでした。 それらを踏まえると、以下のような図になります。 便宜上、図形にA―Iの記号をふっています。
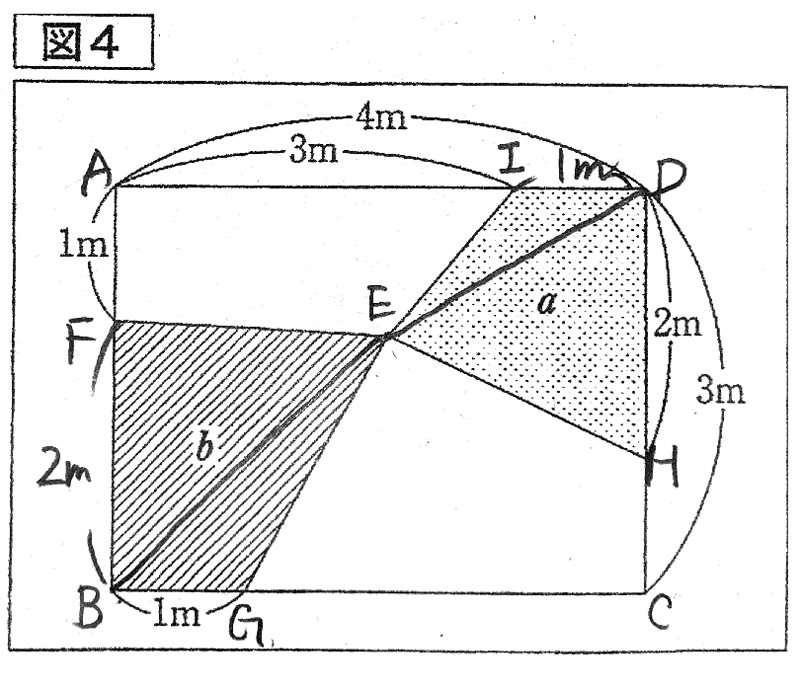
縦×横で面積が求められない四角形は、放置しないで下さい。 そういう時は、面積が求められるように補助線を引いて、三角形に分けることが鉄則です。 「面積問題では、面積が求められるように補助線を引く」ということを覚えて、パッと上記のように補助線が引けるようにしましょう。
さて、ここまできてヒントとなるのが(2)の問題です。 作問者の意図はこうです。「(2)の証明問題を通して、斜線部のような位置関係にある底辺が等しく高さの合計がわかっている2つの三角形の面積の合計は、具体的に出すことが出来ることに気づくだろう。 だから、(3)で利用して欲しい。」です。
具体的に説明していきます。 図4の三角形B G Eと三角形D I Eは底辺をそれぞれB G、D Iとすると高さの合計が3となります。(2)を踏まえると、面積の合計は1×3÷2=3/2となります。 同様に、三角形BFEと三角形DHEも、底辺をそれぞれB F、D Hと置くと、高さの合計が4となり、面積の合計は2×4÷2=4となります。
よって、四角形bの面積は、四角形aとbの面積の合計から四角形aの面積を引いて、3/2+4-5/2=3となります。 最後まで気を抜いてはいけません。 問われているのは四角形bの面積は四角形aの何倍ですかということですから、3÷(5/2)=6/5となります。
攻略法
図形問題の鉄則
繰り返しになりますが、図形問題の鉄則はぜひ覚えて下さい。
1. 情報を全て書き込む
2. 適切な補助線を引く
適切な補助線を引くことにより、色々なことが見えてきます。 以下に、補助線を引くことで気づくことが出来る(2)の模範解答以外の考え方を示します。
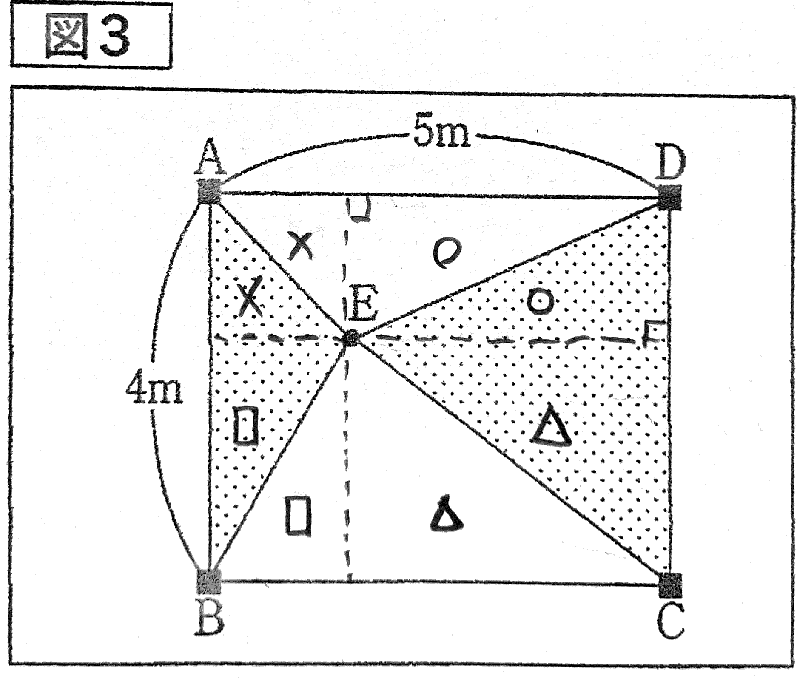
○と○、△と△、□と□、×と×は同じ面積ですので、直感的にもわかりやすく証明することができます。
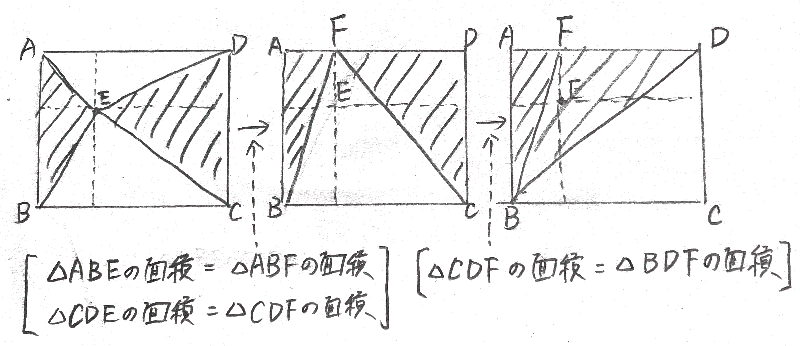
三角形が2つに分かれていることが面倒くさい原因ですから、1つにしてしまおうと考えました。 三角形の平行移動を駆使して、最終的に三角形A B Eと三角形C D Eの面積は三角形A B Dに等しいことが示されます。
証明問題のコツ
証明問題を苦手と考えている人は多いのではないでしょうか? あまり難しく考えないで下さい。 ポイントは、計算式を説明なしに出さないことです。
例えば、今回の問題において、模範解答では「三角形A B Eにおいて、底辺をA Bとして高さを○とおく」と宣言してから「三角形A B Eの面積=4×○÷2」と立式しています。
自分が何に注目してその式を立てているのか、採点者にしっかりとアピールして下さい。
証明問題の点を取る方法として私がお薦めしているのは、模範解答をまねることです。 証明は、書きすぎても時間がかかるし、内容が足りなくとも減点になってしまいます。
手っ取り早くちょうどいい量を知るためには、やはり模範解答をまねることが近道です。 私は、解き直しの時に、毎回自分の解答と模範解答を照らし合わせて過不足を確認していました。
連問にはヒントがある
解説の中でお示ししましたが、連続問題ではたいてい一つ前の問題がヒントになっています。 分からなくなったら、一つ前の問題に戻りましょう。
お薦めの問題集

旺文社 1,078円(税込)
中学入試の「算数・図形」に対応した問題集ですが、各項目(例:面積・辺や周の長さ)の初めの部分に載っている解法と解説が分かりやすいです。 私も、担当の生徒さん達に二華中学校の過去問を解いてもらう際の準備として、この本を使って指導することがあります。




