共通テスト【数学Ⅱ・B】解法 & 勉強方法
皆さん、こんにちは! 仙台市の『名門進学会』家庭教師で、東北大学医学部医学科3年の金子茉央(かねこ まお)です

1. 理解しているか問われる問題が多いので
今日は、大学入試共通テスト【数学Ⅱ・B】で高得点を取るための「解法」&「勉強法」をお伝えします。 共通テストの数学は、ただ問題を解けるかというより理解しているかを問われる問題が多いように感じました。 共通テストらしい傾向です。
どうしてそうなるのかを
この傾向変化に対応するためには、ただ解法を覚えるのではなく、「どうしてそうなるのかを理解する」ようにすると良いかと思います。 普段からそういう練習をしておくと、自ずと共通テストを解くスピードは速くなるはずです。。
2. 出題形式
大問5題。
うち第1問と第2問は必答問題・第3問から第5問のうち2問選択
時間60分・満点100点。
3. 試験の解き進め方
A. 何よりも「時間配分」
【数学Ⅰ・A】の対策と被ってしまうのですが、大事なので繰り返させて頂きます。 まずは、「時間」を厳守することを考えましょう。 只でさえ普段とは異なる緊張感の中、如何に平静を保てるかが勝負の分かれ目です。 模試や過去問を解く時にも、必ず時間配分は意識するべきです。 自分の得意不得意に合わせて、ぜひ決めてみて下さい。
B. 全ての問題に目を通す
解いてみて気が付いたことは、(1)が解けなかったとしても(2)・(3)が解けるように作られている問題もあるということです。 もちろんドミノ倒しのように全てが連鎖的に間違ってしまう問題もありますが、もし最初の方でつまづいてしまったとしても、きちんと全ての問題に目を通し、1問でも多く取れるように粘ってみることが大事です。
C. 見直しの時間は取る!
必ず見直しの時間は取って下さい。 2021年度共通テストは484,114人の受験者がいたそうです。 当たり前ですが、どこの大学の入試よりも受験者数が多く、たった1問間違えただけで、1,000人単位で順位が下がるという話も聞いたことがあります。 ミスがないように細心の注意を払って下さい。
4. 各大問の対策と試験勉強
冒頭の方で、問題の解法を理解すると書きました。 数学は難易度が上がるにつれ、パターン問題が増えてきます。 その手順を丸覚えするのではなく、どういう時にその公式を使っているのか考えることをオススメします。 各大問に触れながら具体的に説明していきます。
A. 大問1(三角関数・指数関数/対数関数)
なぜ合成をするの?
2021年度の共通テスト1問目は、三角関数の合成問題でした。 質問です。 皆さんはどんなときに三角関数を合成したいと思いますか? 私は三角関数のyの範囲を知りたいのに、変数が2つあって分かりにくい時に三角関数の合成をしたいと考えます。
例えば、y=sinθ+√3cosθの形のままではθの変化に対する関数値の変化がわかりにくいですが、y=2sin(θ+π/3)と合成すると関数の値の変化がわかりやすくなります。 最大値や最小値も、下の図のように考えると判断しやすいですのでオススメです。
三角関数合成式の最大値と最小値
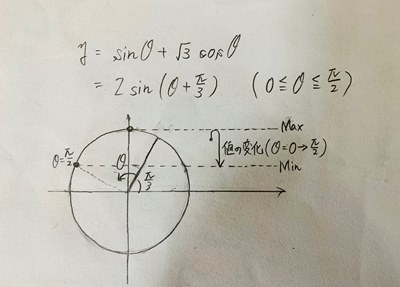
指数関数/対数関数
f(x)=(2^x+2^(-x))/2、g(x)=(2^x ー2^(-x))/2はとても有名な関数です。 グラフの形は覚えておくべきです。 特にf(x) のグラフは線対称であること、g(x)のグラフは点対称であることを知っておきましょう。
また、長い文章の問題には誘導がつきものです。 ぱっと見で的確な解法が思い付くならば必要ないですが、ヒントを読み落とさないようにすることが大切です。
B. 大問2(微分法と積分法)
グラフを描くことの大切さ
私は、1次関数、2次関数、3次関数の問題では必ずグラフを描くようにしていました。 すると、問題が視覚的にイメージできるようになり、出した答えに自信を持つことが出来ます。 答えが正なのか負なのか、交点に対してどちら側にあるか、を確かめるだけでも、テスト中の安心感が全く異なります。
そして、今回の問題では、普段から関数をグラフに変換している人からすれば、容易に解ける問題であったように思います。
まず、2次関数ならばチェックするべきは以下の通りです。
● 上に凸なのか下に凸なのか
● 中心軸が正なのか負なのか
● 頂点のおおよその位置はどこなのか
● y軸との交点はどこか(原点は通るのか)
3次関数ならば、チェックするべきは以下の通りです。
● 変曲点の左右どちらが上に凸なのか
● 重解はあるのか、いくつあるのか
● 極大値、極小値の値
● y軸との交点はどこか
● x軸との交点は正なのか負なのか
漏れがあるかもしれませんが、私の思いつく限りではこんな感じです。 そして、これらの情報がy=ax^3+bx^2+cx+d と与えられた時に、どこの係数で求められるかということを把握しておいて下さい。 例えば、2021年の「ツ」の問題では、y軸との交点における接線を調べるためにはcとdだけに注目しておけば良い、などというようにです。
C .大問4(数列)
数列は、毎年のように出題されている範囲です。 確実に得点源に出来るようにしたいところです。
数列の特徴
数列に苦手意識がある方はいらっしゃるでしょうか? 私の場合、a、b、r、nといったアルフベットを多く用いる数列は、何から手をつければいいのか分からなくなって苦手意識があったことをよく覚えています。
数列は、最後の解き方がパターン化されていることが特徴です。 数列の和や一般項の求め方など公式が様々あると思いますが、知らない数式を自分が公式を使える形に変形しにいくのがポイントです。 様々な問題のパターンを解いていくと、慣れていきます。
2021年の問題では
変形の一つの手段として、例えば等差数列であれば、a_(n+1)=a_n+d(dは公差)、等比数列であればb_(n+1)=b_n・r というようにどんどん置き換えていきます。
今回の問題のように、全ての項にb_(n+1)もしくはb_nが入っているときは、誘導を見なくともb_nで割りたくなる問題です。 もし分からなかったとしても解き方の誘導がついていますので、丁寧に追っていけば解けるはずです。
D .大問5(ベクトル)
計算ミスに注意
ベクトル問題の関門の一つは、計算の煩雑さです。 2021年度の問題でも、根号を用いた計算や二乗をさせる場面がたくさん出てきました。 日頃から計算の練習をしておき、本番でミスが無いようにしましょう。
共通テスト【英語】解法 & 勉強方法
受験生の皆さん、こんにちは! 仙台市の『名門進学会』家庭教師で、東北大学医学部医学科3年の金子 茉央(かねこ まお)です

今日は、大学入試共通テスト【英語】で高得点を取るための「解法」&「勉強法」をお伝えしていきます。 知力を振り絞って書いたので長文になりましたが、その分とても受験生の皆さんの役に立ちます。 ぜひ最後までご覧下さい。
1. 出題形式
A. リーディング
大問6題構成。時間80分。満点100点。
以前まで毎年のように出されていた発音・アクセント問題や文法・語法問題、整序英作文問題などが廃止され、全て読解問題となった。
B. リスニング
大問6題構成。時間30分。満点100点。
イラストやグラフを扱った問題が増えた。
2. 各試験の対策
A. リーディング
時間制限を設ける
まず、一番に気を配るべきは「時間」です。 過去問や予想問題集などで必ず自分なりの時間配分を決めておいて下さい。 模試はその実践です。 もちろん本番はその通りに行くとは限りませんし、特に英語は、新しい文章を読むより大問を終わらせてしまった方が点数を取れることもありますが、時間を決めて取り組むということに慣れておくことが大事です。
そして、実際に時間制限の中で解いてみて解き終わらなかった時は、スピードを上げるために何をすればいいか考える必要があります。 以下に、制限時間内に解き終わらなかった理由別に対策を書き出したので、よく読んで実践して下さい。
スピードを上げるには
問題が解き終わらないのは何故でしょうか? 私が考えつく限りだと、以下の5つの理由が考えられます。
(1) 分からない単語が多い。
(2) 意味がわからない文章がある。
(3) 文章の2度読みをしてしまっている。
(4) 読むスピードが単純に遅い。
(5) 問題を解くときに文章の内容を忘れてしまっている。
皆さんの心当たりはあるでしょうか? 私は、かつて5つ全てに覚えがありました。 それぞれについて、私が実践した対策をお伝えします。
対策(1) 単語力増強
まず「分からない単語が多い」は、率直に語彙力不足です。 少なくともセンター試験レベルと書いてある単語帳(今は共通テスト対策単語帳でしょうか)は一冊買って仕上げて下さい。 出来れば二次試験レベルまでの単語帳を仕上げていて欲しいです。
分からない単語は推測出来ることも
しかし、それでも本番はどうしても意味の分からない単語が出てきます。 そういう単語は、思い切って読み飛ばして下さい。 全体的な文章の意味が掴めてくると、単語の意味が推測できることが多々あります。 自分がある程度単語力つけたなと思った時の分からない単語は大抵の人も分からない単語ですので、本番で焦らないことが大切です。
注釈も覚えておいた方が
とは言え、実際のところ、単語力は青天井です。 後ろの語句注釈に書いてあるものは覚えなくていいやと思うかもしれませんが、世の中には注釈を一切見ない人もたくさん存在します。 その人達と比較したら、ページをめくる分だけの差が出来てしまうのです。 特に高校2年生以下の方は、注釈はいずれ覚えていなくてはならない単語になりますので、覚えてしまった方が後々楽です。
単語さえ知っていれば
個人的な意見ですが、私は、「単語さえ知っていれば、いくら文法を知らずとも、どんな文章でも読めてしまう」と思っています。 単語力は、読解の究極の武器です。
対策(2) 文法力増強
ゆっくり読んだときに「意味が分からない文章がある」のは、文法力不足です。 私は、Z-KAIさん出版の著:風早寛『解体英語構文』という冊子を使っていました。 これに限らず、文法問題集はものによって並び方が違うことが多く網羅的に学ばないと意味がないので、これというものを一冊買って仕上げることをお勧めします。 見た目・手触り・解説の細やかさなどを比較しながらお気に入りの一冊を選んで下さい。
対策(3) 区切って読む
「文章を2度読みしてしまう」という方の中には、文章を頭の中で日本語訳している方がいらっしゃるのではないでしょうか。 日本語訳とは、文章を主語→目的語→述語の順番で読むことです。 英語は、ご存知の通り日本語と語句の順番が違いますので、英語の順番で読んでいくのが大事です。
そこでお勧めなのが、文章を意味の塊ごとにくぎりながら読んでいくことです。 例えば、I rode my bike to school on the hill before my brother arrived. という文章があったら、I rode my bike /to school on the hill /before my brother arrived. といった具合です。
私の学校の先生の
この手法は、私の学校の先生の受け売りなのですが、授業の和訳も意味の塊ごとにやるようになってから大分読む速さが向上しました。 また、読んでいる実感を得られる点でも、区切っていく方法は良かったです。 区切っている範囲は一目で意味がわかる量なので、慣れると区切り線を入れるのと同じ速さで読むことが出来ます。
対策(4) とにかく量をこなす
読むスピードが単純に遅い人は、おそらく長文を読むことへの慣れが足りないのだと思います。 一文章を読むことと長文を読むことは大きく異なります。 体力も集中力も必要です。 慣れるために私はZ-KAIさん出版の著:風早寛「速読英単語」を活用していました。 これはシリーズもので、難易度に合わせて色々な種類がありますので、興味をもった方はぜひ調べてみて下さい。
対策(5) 問題を見てから本文へ
「問題を解くときに文章の内容を忘れてしまっている」ということに私はひどく苦しめられたものでした。 文章を読み直している時間や該当箇所を探している時間は、最も無駄な時間であると言えます。 もし、同志の方がいらっしゃいましたら、ぜひ問題文に軽く目を通してから本文に臨んでみて下さい。
問題を解くのと並行しながら
チェックすることは2つです。 1つ目は、問題が局所部分を見れば解ける問題なのか、要約のような文章全体の俯瞰問題なのかを把握すること、2つ目は、問題を解くためのキーワードを見つけておくことです。 共通テストの問題は、多くが文章に書いてある順に出題されていますので、問題を解くのと並行しながら文章を読んでいっても良いです。
共通テストは記号問題なので違いますが、二次試験では要約問題が出題されることもあります。 そういうときは、段落ごとに軽くまとめを書いておくことをお勧めします。 読み返しを大幅に防げます。
B. リスニング
今までの努力の積み重ね
リスニングは、身も蓋もない話をすると、今までどれだけ英語に触れてきたかに能力が比例します。 私がそうだったのですが、受験間近になって慌ててどうにかしようとしても、あまり伸びは期待できません。 私の友達の話を聞く限りでは、基礎英語を中1の時から毎日コツコツ聞いてきた人がやっぱり強いです。 ですが、伸びないからといって捨ててよい科目ではないです。
共通テストで求められるもの
共通テストでは、かつて2回読まれていた音声を1回しか流さなくなり、表やグラフの照らし合わせなどの問題が増えるという大幅な改題が生じました。 瞬時に英語を聞き取る能力、正確に聞き取る能力、理解して整理する能力が必要とされています。
克服するためには
まずは、音声ソフトを利用して正しい英語の発音を聞く機会を増やして下さい。 単語を習得するときに音と一緒に覚えてこなかった人は、初期に習った単語であっても意外と発音を間違えて覚えていることがあるかと思います。
次に、聞きながらメモを撮る練習です。 私はディクテーションを学校でやらされていました。 聞き漏らしを2回目で集中的に聞くということが出来なくなったので、聞く行為とメモを取る行為を並行する練習は繰り返し行っておく必要があります。
3. 最後に
ここまで読んできて、いかがだったでしょうか? センター試験から共通テストに移行する中で、一番大きく変化したのが「英語」であるように思います。 新型コロナウイルスの大流行や教育改革に直面してとても大変な世代だとは思いますが、受験生の皆さんどうか勉強頑張って下さい。
共通テスト【数学Ⅰ・A】解法 & 勉強方法
受験生の皆さん、こんにちは! 仙台市の『名門進学会』家庭教師で東北大学医学部医学科3年の金子 茉央(かねこ まお)です

今日は、大学入試共通テスト【数学I・A】の、高得点を取れる「解法」&「勉強法」をお話し致します。 数学に関しては、難易度や問題構成は以前のセンター試験とあまり変わりませんが、少し雰囲気が変わり、考えさせられる問題になっています。
1. 出題形式
大問5題構成。
第1問、第2問は必答。第3~5問はいずれか2問を選択して解答する。
時間70分、満点100点。
2. 試験の解き進め方
全ての試験について言えることですが、テスト中に一番守らなくてはならないもの、それは「時間」です。 大問5題なので、私は各大問につき最大15分ずつ割り振っていました。 第1問と第2問は比較的典型問題なのでなるべく早く解くようにし、たまに捻った問題の出る第3〜5問に時間を割くようにしていました。
必ず見直しの時間を取る
そして忘れてはならないのは、見直しの時間です! 共通テストの何より恐ろしいところは、ミスをしてしまうとその問題を解ける人が一定数いるために差をつけられてしまうところです。 特に、本番の極限に緊張した環境では何が起こるか分かりません。 必ず見直しの時間は取って下さい。
ミスをしにくい問題を選択する
皆さんは、選択問題何を選んでいますか? 選び方の基準は、問題の好み、得意なもの、ぱっと見の解きやすさなど色々あると思いますが、私は基本的に整数の性質と図形の性質を選んでいました。 なぜならば、答えを出したときにミスをしていない確信が持ちやすいからです。
もちろん、問題の種類によっては確率を選ぶこともありましたが、ミスを減らすべく選択問題を選ぶようになってからは、大分数学の正答率が上がっていきました。 ここら辺の判断基準については、また後ほど書きます。
3. 各大問の対策と試験勉強
私は、センター試験・共通テストの数学は、公式の典型的な使い方を如何に正しく理解しているかが鍵だと思っています。 点数が取れないとき、やるべきことは過去問や予想問題の解説を読み、問題と対応させることです。
どういう条件が出ているときにどういう公式を使っていくのかがおおよその流れがあって、問題の中できちんと誘導されていることに気付くはずです。 以下では各大問についてお伝えしていきます。
A. 大問1(数と式、二次関数、図形と計量)
二次方程式のポイント
まず、二次方程式についてです。 二次方程式を解くコツは、余計な係数を省いてグラフをシンプルに見てグラフの形をイメージすることです。「Y=Ax2+Bx+C」*の形になっているはずです。 2021年の問題では2×2+(4c-3)x+2c2―c―11=0という問題が出ましたが、この場合もA=2、B=4c-3、C=2c2―c―11と見なすことができます。
以下のルールを覚えて下さい
今回の問題でもありましたが、cにある値を代入することは、*のグラフの係数を変化させていることに過ぎません。 係数が変わることは、グラフが平行移動していることに過ぎません。 これを理解するには、以下のルールをぜひ覚えて下さい。
● A>0なら下に凸(逆は逆)。 Aはグラフの形を決める。
● B/A>0ならグラフの軸は負の領域(逆は逆)。 Bが変化するとグラフはx軸方向に平行移動する。
● C>0ならy切片は正(逆は逆)。 Cが変化するとグラフはy軸方向に平行移動する。
これらのルールは、恐らく二次方程式を習ったころに言われたことだと思います。 当たり前のことだと思われるかも知れませんが、この情報さえあればy―xグラフのおおよその位置や動きが把握できます。 そして、求めた答えが大体あっているか視覚的に確認出来ることにより、ミスを減らし自信を持って次の問題に進むことが出来ます。
図形問題のポイント
次に、図形の問題です。 2021年の問題は正方形や三角形の面積をcosθやsinθの公式に絡めて解くという面白い問題でした。 図形の問題は、まずわかる限りの情報(角度や辺の長さ)を図の中に書き込んでください。 その上で、初めて問題を解き始めます。
(3)の問題を例に取ると
2021年(3)の問題を例に取ってみると、△AIDの面積=1/2ac・sin(180-B)=1/2ac・sinB=△ABCの面積となります。 同様に他の三角形も求めていくと、結局△ABCの面積に行き着くという問題でしたが、きちんと情報を書き込んでいくことで三角形の面積を迷わずに導き出すことが出来ます。
(2)・(4)の問題は
また、(2)・(4)の問題は、三角関数の公式に注目します。(2)の問題では、cos A=(b^2+c^2ーa^2)/2bcの余弦定理に注目すると、Aが鋭角か否かによって面積の大小関係が定まることが分かりますし、(4)では外接円の半径が2r=a/sinAで求められることに気づけば苦労せずに問題を解くことが出来ます。
思考力問題に対応するために
共通テストは、思考力が問われるテストと言われています。 通り一遍等の解き方で問題に取り組んでいても解けない問題が、これから先出てくるかもしれません。
色々な解き方を知っておく
私は、学校の授業の一環で、典型問題と言われる易しい問題をなるべく多くの別解を用いて解くということをしていました。 一つの問題を解く際に別解を知っていると言うことは、その問題を色々な視点から見ることが出来ると言うことです。 すこぶる煩雑で時間を浪費してしまう解き方もあれば、魔法のように一瞬で答えが導き出せる解き方もあります。
最良のアプローチをする
受験は、時間との勝負です。 毎回煩雑な解き方をしていれば解き終わらないし、一方で魔法の解き方は使える場合が限られていることが多いです。 そこで、どちらも知っていることが求められます。 自分の知っているアプローチの中からもっとも賢い解き方を選択し、煮詰まった時に最終手段として煩雑な解き方を持っていることが理想です。
もちろん言うは易しなので、そう簡単に問題を達観することはできませんが、余裕がある時に別解を知っておこうとする努力は大切です。 私は、模試の問題で解けた問題であっても一応解説に一通り目を通すようにしていました。
B. 大問2(二次関数、データの分析)
新規単位は定義を確認
2021年度の問題では、タイム・ピッチ・ストライドと言う見慣れない単位が出てきました。 しかし、見慣れない言葉に出会っても焦らず落ち着いて考えることが大事です。 私は、新しく単位を認識する時、必ずその単位を定義する式を確認します。
今回であれば、ストライド(m/歩):一歩で何m進めるのか、ピッチ(歩/秒):1秒で何歩歩けるのか、です。 こうやって単位について自分の頭を整理しておくと、その後に考えさせられる平均速度:1秒に何m進めるのかについても、自然とストライドとピッチを掛け算すれば良いと考えられます。
データ分析は慣れ
まずは、最低限の知識を入れることです。 過去問をいくつか見てみると、自ずと知っておくべきデータの値が分かってくると思います。 私は、この範囲に苦手意識を持っていて模試を解くたびに何かしらの間違いをしていましたが、繰り返し問題に触れるうちに、丁寧に数えてグラフを対応させていけば必ず解けること、そしてパターン問題が多いことに気づきました。
丁寧に解けば解けると言いましたが、これは時間制限のある共通テストですので、いかにこの範囲に時間を割けるかも課題です。
C. 大問3(場合の数と確率)
誘導に乗ること
2021年は、条件付き確率の問題でした。 問題自体は典型問題で、難易度は高くないですが、ポイントは問題の誘導に如何にきちんと乗ることが出来るかです。 会話文の中で作問者が解答者に考えさせたいことを理解して、丁寧に解いていきましょう。 そして、これはチャンスでもあります。
誘導があるということは、普段の考え方とは別の解き方をさせたいと言うことです。 それは、普段の解き方でも解けばもれなく確かめ算をすることになり、答えが一致したら安心して次の問題に進むことが出来ます。
全体の事象の意識
私は、確率や場合の数は、全体の事象を意識して解くようにしていました。 具体的に言うと、確率であれば各事象を足したら1になることであり、場合の数であれば全ての事象を書き出すと言うことです。 もちろん時間のかかる方法ですので最初は普通に解きますが、残りの事象を把握しておくと答えへの自信に繋がります。
D. 大問4(整数の性質)
選択問題としておすすめ
基本的に典型問題が多く、問題文では様々なゲームが提示されつつも、一次不定方程式の整数解を導く問題となることが多いです。 不定方程式を満たす数字を調べること、xとyの一般式を出すこと、xとyの解の範囲に注意することが出来れば、大体の問題は誘導に乗って解いていけるはずです。 大きい値になった時には、計算ミスには注意して下さい。
比較的解きやすくミスも生じにくい上、方程式に当てはめて計算すれば確かめ算も出来るので、私はこの大問を選ぶことが多かったです。
E. 大問5(図形の性質)
完答が難しい
図形は、得意不得意分かれるところだと思います。 個人的な感想としては、テスト中の緊張感の中では気付くべきことに気付けず完答が難しかったので、選択することは少なかったです。
図は正確に
図形問題対策としては2つあります。1つ目は図を正確に書くことです。 長さの大小のみならず角度も鋭角、鈍角、直角いずれなのか正確に書きます。 特に、有名な直角三角形は必ず覚えて下さい。 直角であることに気づけるか否かは、正答率を大きく左右します。
公式は頭に叩き込む
問われ方に対する公式の用い方をきっちり把握しておくことは、とても大事なことです。 例えば、4つの点が円上にあることを示すには?と聞かれたら、方べきの定理の逆か円周角の定理の逆を使えばいいのだなというようにです。 図形上に情報は無限にありますが、使うべき公式は限られています。
公式のアテを初めにつけることが出来れば、図形問題は大分解きやすくなります。
4. 最後に
長くなってしまいましたが、いかがだったでしょうか? 受験生の皆さんの数学試験対策の手助けに少しでもなれば、私としてもとても幸いです。 皆さんは、カリキュラムの変わり目に当たってしまってとても大変な思いをしているとは思いますが、ぜひ頑張って下さい。
東大などの【数学】考え方&解法
受験生の皆さん、こんにちは! 仙台市の『名門進学会』家庭教師で東北大学医学部医学科2年の金子 茉央(かねこ まお)です

1. お疲れ様でした!
皆さんは、怒涛の日々が過ぎ去り、ようやく一息つけた頃でしょうか? 中には、気持ちを切り替えて、後期試験に向けて勉強に取り組んでいる方もいらっしゃるのでしょうか? 何はともあれ、本当にお疲れ様でした。
サクラ咲ケの赤べこ

2. 難問に挑戦した過去
皆さんは、東大の問題を解いたことありますか? 一度触れたことがある人ならお分かりだと思いますが、東大の問題は期待を裏切らずものすごく難しいです。 私の志望校は高3の春に決まりましたが、難問を解く力を身につけるべく東大・京大・東工大といった難問を出すことで有名な大学の問題も積極的に解いていました。
受験目前には東大の問題でも
中には何度問題文を読んでも手も足も出ない問題すらあって、始めの頃は気が遠くなるような思いをしたことをよく覚えています。 でも、私は受験を目前に控えた頃には、東大の問題に対して以前のような忌避感は覚えなくなっていました。
東大などの赤本

3. 難問を解くときの考え方・解法
どうしてなのか? そこで、今回は、「数学」や「理科」の難しい問題を解く時の考え方や解法についてお話ししていきます。
A.「難問」へのアプローチ
「難問」と言われる問題は、何がその問題を難問たらしめているのでしょうか? いかに大学の教授が作った難しい問題といえども、高校生の知っている知識や公式で解けなくてはなりません。 高校生の知っている知識や公式を用いて解くことの出来る数学の典型は、すなわちチャートの例題です。
青チャートの例

使ったことのある人ならお分かりだと思いますが、チャート(私は青チャートを用いていました)は、公式ごとに定型の問題文に対して、最も効率の良い解き方が示されています。 そして私は、ほとんどの難問は何らかの閃きや解釈によって、これらのパターン問題に「落とし込む」ことが出来ると思っています。
B. 自分の知っている問題に「落とし込む」
手も足も出ないのは、自分が見たことがない問題だからです。 ならば、自分の知っている「チャートのパターン問題に落とし込める」ように頑張れば良いのです。 そう考え始めてからは、見たことのない問題であっても「解ける訳がない!」という忌避感を感じなくなりました。
いわゆる難関校の問題は
とは言っても、青チャートの例題はしっかりやり込めば偏差値60くらいになるので、パターン問題と言っても皆が解けるわけではありません。 そこを当たり前に解けるものとして提示してくるのが、いわゆる難関校の問題であるように感じます。
C. 自分にあったレベルから着実に
今、難関校の問題が全く解けないと感じる人は、是非とも「自分がどの段階でつまずいているのか」解答を読んで確かめて下さい。 難問を自分の知っているパターン問題に落とし込む所で手こずっているのか、それとも次の段階のパターン問題をきちんと身につけていないのか。
よく使っていた問題集

もう一度解き直して
後者である場合は、チャートレベルの問題集を今一度解き直して下さい。 数学の問題集は、無闇に難易度の高いものに手をつけてはいけません。 難しい問題集は、その1ランク下の問題集が解けることを前提として構成されていますから、それがきちんと解けるようになってから次に進むべきです。
忌避感を和らげられたら
難問への取り組み方について自分なりの考え方をお伝えしてきましたが、いかがでしたでしょうか? もちろんこれは1個人の意見なので、皆さんも自分なりの考え方で難問にアプローチして頂ければと思います。 私の勉強法で、皆さんの忌避感を少しでも和らげられたら幸いです。 最後まで読んで頂きまして、有難うございました。









