
宮城県立高校入試:数学の合格勉強法
過去問の内容を踏まえながら、問題ごとの具体的な解法や戦略的勉強方法について述べます。
1数学の問題構成と概略
宮城県立高校入試・数学の問題構成は、以下の通りです。
| 第一問 | : | 小問集合(計算問題が中心) |
|---|---|---|
| 第二問 | : | 関数・空間図形・数と式・データの活用(基本問題が中心) |
| 第三問 | : | データの活用・関数(身の回りの事例) |
| 第四問 | : | 平面図形(記述式の図形の証明問題) |
宮城県立高校入試は、レベルの高いコースを持つ私立高校などと比べると比較的やさしい問題が多いです。 簡単な問題をミスなく確実に拾って行くことが、とても大切になってきます。 加えて、記述式の証明問題や少し難易度の上がる最後の図形問題を取れるようになることが、合格への道です。
参考書のご紹介
また、入試問題を解くのに必要な事柄を分かりやすくまとめて記載している「参考書」をここでご紹介しますので、合わせてご覧下さい。この本を読んで中の問題を解けば、中学校の3年間で生じた知識の穴を比較的短い時間で埋めることができます。

文理 1,210円(税込)
2ミス=命とり
宮城県の高校入試は、易しい問題が多いのでミスをしてはいけないと書きました。 それは、逆に捉えると、ミスをしたら周りとの差がついてしまうということです。
ですから、問題を解きながらなるべくミスをしてしまわないように対策を練る必要があります。 私がミスをしないためにやっていたことを、3つご紹介します。
A.余白に記す計算の過程は左から右、上から下へ書く
焦っているとき、計算式を余白のあちこちに書いて、後から見返した時にこの計算はどこから出てきたの!?ということがありませんか? 私はよくそれをやってしまっていたのですが、ミスをしてはいけない問題ほど計算の過程は後から見た時にわかるように残しておくべきです。
なぜなら、限られた時間の中で見直すためには、自分の解いた痕跡を辿っていくのが一番効率がよいからです。 そして、計算の痕跡を残しておくと筆算などの間違いに気づきやすくなる上に、自分が計算のどの段階からやり直せばいいか明白にすることができます。
B.解き直しは別解で解く
見直すときに余り時間がない時は、自分の計算の痕跡を辿って下さい。 但し、時間がある時はぜひ別解で解き直すことをお勧めします。 別の解法で解いて答えが同じになったら、その問題は絶対に合っていると確信を持つことが出来ます。
私は、テストの解き直しの際、合っていた問題でも軽く解説を読んで自分と別の解き方をしている際はなるべくチェックするようにしていました。 また、抽象的な答えを導き出す問題では、導き出した答えに具体的な値を入れて確かめ算をすることも有効です。 具体例として2022年度の第二問1(2)と3(2)を以下に示します。
第二問1(2)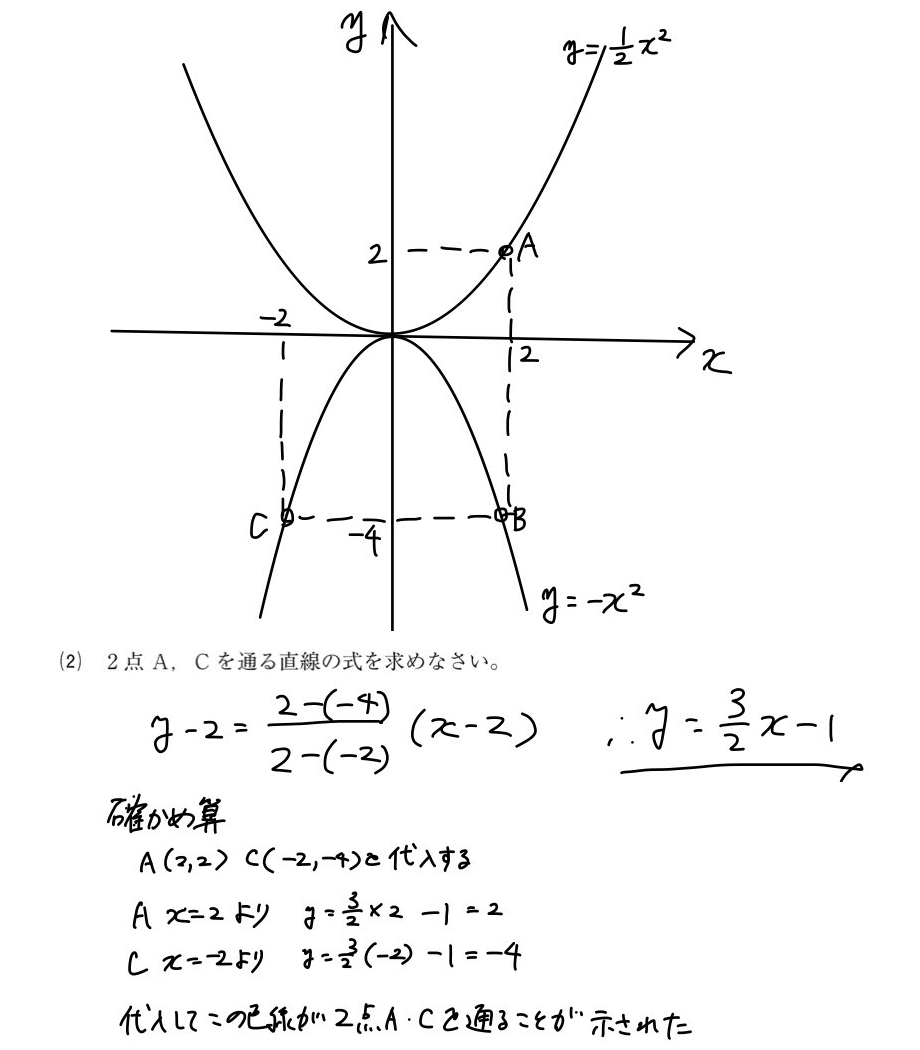 |
第二問3(2) |
C.ミスをミスで終わらせない
どれだけ自分が理解していようとも、ミスして落とした問題は分からなかったのと同じことになってしまいます。 そして、数多のテストの解き直しを繰り返すうちに気がついたことは、自分のミスには傾向があるということです。
解き直しをあまりしたことないという方は、ぜひ何回かやってみて下さい。 何でこんな間違いを?またやったのか…という感想は免れないでしょう。 自分のミスの傾向を掴み、どうしてそのミスをしやすいのかを考えてみて下さい。
ちなみに私は、焦っている時に計算式を隅の方に小さく書き、数字を読み間違えて計算を間違えるパターンが多かったです。 A.の対策は、このパターンを解決するために考えたものでした。
3図形の証明問題
図形の証明問題って何から書けば分からない…という方はいませんか? その中でも、証明方法が分からない人と証明を書いても減点される人の2通りいるかと思います。 それぞれについて対策を書きます。
A.証明方法が分からない人の対策
数学は、とても厳格な学問です。 一つの事実を証明するとき、世界中の人が納得するものを使って証明しなくてはなりません。 ですから、逆に言えば、そんなに信用がある方法は限られているのです。
問題をたくさん解いてみて下さい。 証明問題の解法は、限られた方法しかありません。 例えば三角形の相同を証明するときは、3組の辺の比が全て等しいこと、2組の辺の比とその間の角の大きさが同じであること、2組の角がそれぞれ等しいことの3通りしかありません。 この中のどれかなと考えながら問題を眺めることが出来れば、解き方に迷わなくなってくるはずです。
B.書いても減点される人の対策
証明問題は、セリフの言い回しから論理展開に至るまで型が決まっています。 その最適解が模範解答に載っていますので、書いても減点されてしまう人は、ぜひ模範解答をまねして書く練習をして下さい。

くもん出版 1,540円(税込)
4公式という武器を使いこなせ!
皆さんは、数学をどのように勉強していますか? 時間制限がある中で数多の計算をしなくてはいけないわけですから、数学は「効率」が命です。 そして、効率とは、「公式を如何に使いこなしていくか」とも言い換えられます。
私は、公式を問題という敵に立ち向かうための武器だと思っています。 遠くから攻撃してくる敵には弓矢を用いるし、接近戦が得意な敵には剣を用いるというように、敵の性質によって効果的な武器は違います。
数学でも、計算問題には分配法則、図形問題には円周角の定理というように公式を使い分ける必要があります。 そして、この使い分けには慣れが必要です。 先生から新しい公式を学んでも、それだけでは真新しい武器をもらったに過ぎません。 武器はちゃんと使う練習をしなくては、いざというときに使う判断が出来ないのです。
私は、数学の勉強を2段階に分けて考えていました。 授業は、新しい解法を理解するフェーズです。 そして、家に帰って練習問題を解いて、その公式をどうやって使うのか、どういう時に使うのかを確認していました。 2022年度の問題を通して具体的に見ていきましょう。
(詳細は、過去問集2022年度第4問の最初からご覧下さい。)
第四問4:線分E Dと線分D Gの長さの比を求めなさい。
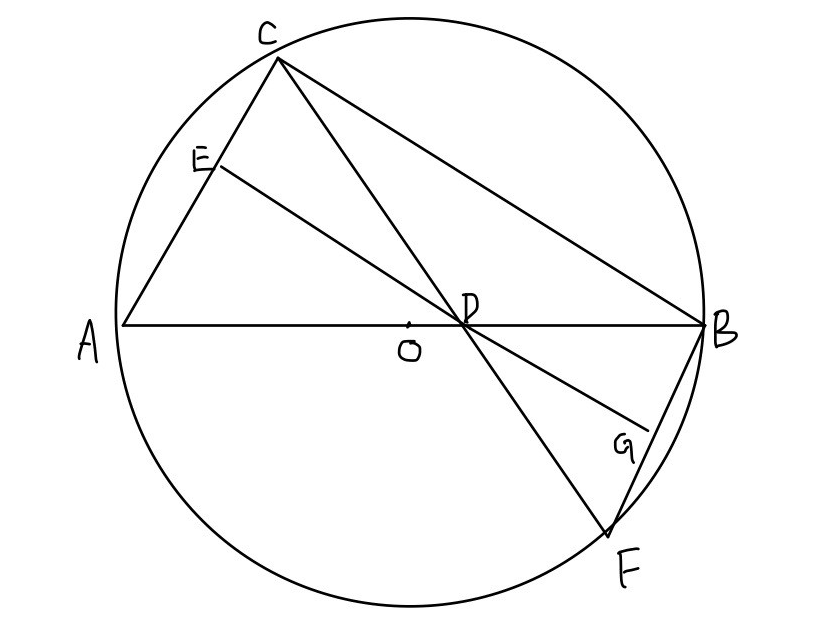
円の中に三角形があります。 この時点で、円周角の定理、方べきの定理、接弦定理などを頭に浮かべましょう。 そして、この問題は辺の比を求める問題ですから、相似な三角では相似比は三組の辺のどれでも成り立つことを利用しようと考えます。 そうすると、以下のような情報が出て来るので、図に正確に書き込んでいきます。
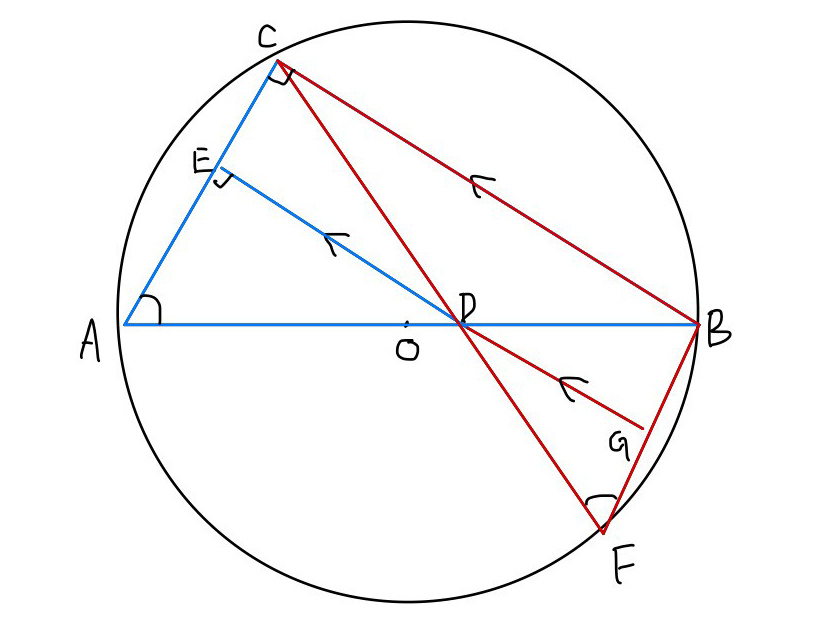
逆算して考えていきます。 まず、線分の比を相似な三角形において相似比が3組のどれでも成り立つことを利用しようと考えますが、E D:D Gに対応する相似な三角形はありません。
そこで、何か間接的に利用できるものはないかと考えると、△A D E∽△A B Cであること、△F D G∽△F C Bであることから、E D:C B、D G:C Bから線分の比を出すことが出来そうだと気づきます。
また、相似な三角形の関係からE D:B C=A D:A B、D G:C B=F D:F Cに置き換えること出来、唯一値の分からないF Dの長さは、A D、B D、C Dの値と方べきの定理から求めることが出来ます。
これらの筋道を逆算して立ててから順序よく解いていくと、E D:D Gは14:9であることが導き出されます。 公式を頭に思い浮かべることが出来ると、問題の流れを逆算して合理的に答えを導くことが可能になります。

旺文社 1,155円(税込)
5最後に
以上、いかがでしたでしょうか? 少しでも受験生の皆さんのお役に立つことが出来れば、幸いです。




