共通テスト【数学Ⅱ・B】解法 & 勉強方法
皆さん、こんにちは! 仙台市の『名門進学会』家庭教師で、東北大学医学部医学科3年の金子茉央(かねこ まお)です

1. 理解しているか問われる問題が多いので
今日は、大学入試共通テスト【数学Ⅱ・B】で高得点を取るための「解法」&「勉強法」をお伝えします。 共通テストの数学は、ただ問題を解けるかというより理解しているかを問われる問題が多いように感じました。 共通テストらしい傾向です。
どうしてそうなるのかを
この傾向変化に対応するためには、ただ解法を覚えるのではなく、「どうしてそうなるのかを理解する」ようにすると良いかと思います。 普段からそういう練習をしておくと、自ずと共通テストを解くスピードは速くなるはずです。。
2. 出題形式
大問5題。
うち第1問と第2問は必答問題・第3問から第5問のうち2問選択
時間60分・満点100点。
3. 試験の解き進め方
A. 何よりも「時間配分」
【数学Ⅰ・A】の対策と被ってしまうのですが、大事なので繰り返させて頂きます。 まずは、「時間」を厳守することを考えましょう。 只でさえ普段とは異なる緊張感の中、如何に平静を保てるかが勝負の分かれ目です。 模試や過去問を解く時にも、必ず時間配分は意識するべきです。 自分の得意不得意に合わせて、ぜひ決めてみて下さい。
B. 全ての問題に目を通す
解いてみて気が付いたことは、(1)が解けなかったとしても(2)・(3)が解けるように作られている問題もあるということです。 もちろんドミノ倒しのように全てが連鎖的に間違ってしまう問題もありますが、もし最初の方でつまづいてしまったとしても、きちんと全ての問題に目を通し、1問でも多く取れるように粘ってみることが大事です。
C. 見直しの時間は取る!
必ず見直しの時間は取って下さい。 2021年度共通テストは484,114人の受験者がいたそうです。 当たり前ですが、どこの大学の入試よりも受験者数が多く、たった1問間違えただけで、1,000人単位で順位が下がるという話も聞いたことがあります。 ミスがないように細心の注意を払って下さい。
4. 各大問の対策と試験勉強
冒頭の方で、問題の解法を理解すると書きました。 数学は難易度が上がるにつれ、パターン問題が増えてきます。 その手順を丸覚えするのではなく、どういう時にその公式を使っているのか考えることをオススメします。 各大問に触れながら具体的に説明していきます。
A. 大問1(三角関数・指数関数/対数関数)
なぜ合成をするの?
2021年度の共通テスト1問目は、三角関数の合成問題でした。 質問です。 皆さんはどんなときに三角関数を合成したいと思いますか? 私は三角関数のyの範囲を知りたいのに、変数が2つあって分かりにくい時に三角関数の合成をしたいと考えます。
例えば、y=sinθ+√3cosθの形のままではθの変化に対する関数値の変化がわかりにくいですが、y=2sin(θ+π/3)と合成すると関数の値の変化がわかりやすくなります。 最大値や最小値も、下の図のように考えると判断しやすいですのでオススメです。
三角関数合成式の最大値と最小値
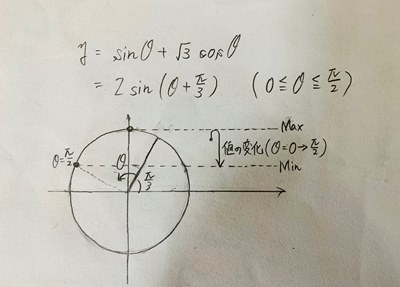
指数関数/対数関数
f(x)=(2^x+2^(-x))/2、g(x)=(2^x ー2^(-x))/2はとても有名な関数です。 グラフの形は覚えておくべきです。 特にf(x) のグラフは線対称であること、g(x)のグラフは点対称であることを知っておきましょう。
また、長い文章の問題には誘導がつきものです。 ぱっと見で的確な解法が思い付くならば必要ないですが、ヒントを読み落とさないようにすることが大切です。
B. 大問2(微分法と積分法)
グラフを描くことの大切さ
私は、1次関数、2次関数、3次関数の問題では必ずグラフを描くようにしていました。 すると、問題が視覚的にイメージできるようになり、出した答えに自信を持つことが出来ます。 答えが正なのか負なのか、交点に対してどちら側にあるか、を確かめるだけでも、テスト中の安心感が全く異なります。
そして、今回の問題では、普段から関数をグラフに変換している人からすれば、容易に解ける問題であったように思います。
まず、2次関数ならばチェックするべきは以下の通りです。
● 上に凸なのか下に凸なのか
● 中心軸が正なのか負なのか
● 頂点のおおよその位置はどこなのか
● y軸との交点はどこか(原点は通るのか)
3次関数ならば、チェックするべきは以下の通りです。
● 変曲点の左右どちらが上に凸なのか
● 重解はあるのか、いくつあるのか
● 極大値、極小値の値
● y軸との交点はどこか
● x軸との交点は正なのか負なのか
漏れがあるかもしれませんが、私の思いつく限りではこんな感じです。 そして、これらの情報がy=ax^3+bx^2+cx+d と与えられた時に、どこの係数で求められるかということを把握しておいて下さい。 例えば、2021年の「ツ」の問題では、y軸との交点における接線を調べるためにはcとdだけに注目しておけば良い、などというようにです。
C .大問4(数列)
数列は、毎年のように出題されている範囲です。 確実に得点源に出来るようにしたいところです。
数列の特徴
数列に苦手意識がある方はいらっしゃるでしょうか? 私の場合、a、b、r、nといったアルフベットを多く用いる数列は、何から手をつければいいのか分からなくなって苦手意識があったことをよく覚えています。
数列は、最後の解き方がパターン化されていることが特徴です。 数列の和や一般項の求め方など公式が様々あると思いますが、知らない数式を自分が公式を使える形に変形しにいくのがポイントです。 様々な問題のパターンを解いていくと、慣れていきます。
2021年の問題では
変形の一つの手段として、例えば等差数列であれば、a_(n+1)=a_n+d(dは公差)、等比数列であればb_(n+1)=b_n・r というようにどんどん置き換えていきます。
今回の問題のように、全ての項にb_(n+1)もしくはb_nが入っているときは、誘導を見なくともb_nで割りたくなる問題です。 もし分からなかったとしても解き方の誘導がついていますので、丁寧に追っていけば解けるはずです。
D .大問5(ベクトル)
計算ミスに注意
ベクトル問題の関門の一つは、計算の煩雑さです。 2021年度の問題でも、根号を用いた計算や二乗をさせる場面がたくさん出てきました。 日頃から計算の練習をしておき、本番でミスが無いようにしましょう。









